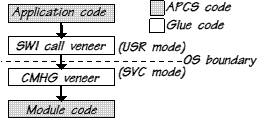
Relocatable modules for RISC OS may be written either in C or in assembly language. However, because modules operate below the boundary between user programs and the operating system, special tools are needed to protect compiled C code from its environment.
Compilers for high-level languages such as C and Pascal produce code that conforms to the ARM Procedure Call Standard. The APCS defines strict rules regarding register usage, procedure call/return, stack backtrace and software stack-limit checking. In contrast, operating system code and extension modules written in assembly language are coded more freely, use the non-extensible SVC mode stack, and do not perform stack limit checking.
A tool called CMHG (C Module Header Generator) creates
a module header, initialisation/finalisation code and a set
of entry and exit veneers to interface the C run-time
environment with low-level system entry points such as SWIs,
CLI commands and IRQ handlers. The code to implement the
functionality of the module is written in C, and must be
compiled with a special compiler option to allow
static data to be separated from the module code and
multiply-instantiated.
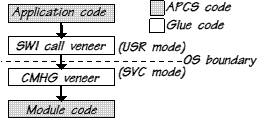
The call overheads in implementing a C library as a module.
Modules written in C tend to be both larger and slower than modules written in assembly language, partly because code generated by compilers is less the optimal, but also because of the amount of code required to interface with the C library upon initialisation and the necessity of veneers to insulate the APCS run-time environment from the operating system level. Software stack-limit checking also imposes a minor performance penalty on every function call.
For these reasons, and particularly because speed is paramount for this application area, I decided to choose ARM assembly language for the implementation of the GL module. Potential portability is really not a consideration, since OpenGL implementations for most other platforms already exist, and in any case the need to obtain optimal performance on ARM systems would probably preclude this.
I had access to three different ARM code assemblers, the BASIC assembler, Acorn's ObjAsm and Nick Roberts' ASM. I investigated the features of each and enquired within the programming community as to their relative merits before deciding which to use.
![]() BBC BASIC has a built in
assembler, which I have used for previous programming
projects. Its main advantage as described by Philip Ludlam is
that you can do "...neat BASIC tricks. Things like calling
functions within the assembler code or looping through loops
to generate data or code." [25] Thus the BASIC assembler
effectively supports macros, conditional assembly and
repetitive assembly 'for free', using the power of the
underlying language.
BBC BASIC has a built in
assembler, which I have used for previous programming
projects. Its main advantage as described by Philip Ludlam is
that you can do "...neat BASIC tricks. Things like calling
functions within the assembler code or looping through loops
to generate data or code." [25] Thus the BASIC assembler
effectively supports macros, conditional assembly and
repetitive assembly 'for free', using the power of the
underlying language.
The main disadvantage of the BASIC assembler is that it does not output linkable object files. Therefore large programs cannot be split into separately generated code modules, and it is not possible to link the output with external code libraries or object files produced by C and other compiled languages.
![]() Acorn's ObjAsm was
part of their commercial C/C++ product, which also includes a
C compiler, C++ translator, debugger and linker.
ObjAsm supports macros, conditional assembly
(
Acorn's ObjAsm was
part of their commercial C/C++ product, which also includes a
C compiler, C++ translator, debugger and linker.
ObjAsm supports macros, conditional assembly
(IF...ELSE...ENDIF), repetitive assembly
(WHILE..WEND) and sophisticated symbolic
capabilities (arithmetic, logical and string variables).
According to Weiss Niklaus it has the advantage over the
BASIC inline assembler that it can generate debugging data
for use with DDT27, an interactive debugging tool. [25]
ObjAsm generates object files in the standard AOF format28. These can be linked to other object files (including those produced by the C compiler) by any AOF linker, such as Acorn's Link or the freeware DrLink alternative by David Daniels.
Lee Johnston expresses some doubt about the future state of support for ObjAsm: "I wouldn't say that ObjAsm is being actively maintained, or rather that it is but the latest versions don't seem to be available outside of Pace." [25]
![]() Nick Roberts' freeware
ASM is a simple ARM code assembler. Like ObjAsm it
produces AOF files suitable for use with the linker, but it
doesn't support repetitive assembly or many of
ObjAsm's complex symbolic capabilities. Simple
conditional assembly is supported however, using
Nick Roberts' freeware
ASM is a simple ARM code assembler. Like ObjAsm it
produces AOF files suitable for use with the linker, but it
doesn't support repetitive assembly or many of
ObjAsm's complex symbolic capabilities. Simple
conditional assembly is supported however, using
IFDEF/IFNDEF directives to test whether
certain assembly-time flags are defined or undefined. Macros
are supported.
The main feature that ASM has over ObjAsm is that it supports structures for organising blocks of memory. Lee Johnston describes how you "...load a register with the address of an instance of that structure and then access all the fields using a named label rather than offset. It's quite nice." [25]
I wanted to structure my project as a series of independently-compilable code modules, and wanted the option of statically linking these with test programs written in C. These requirements pointed to using one of the AOF generating assemblers.
I was attracted by ASM's support for named data
structures29. I
anticipated that these would be particularly invaluable in
writing a module, since all data must be accessed via a
workspace pointer for the current instantiation rather than
directly. Being able to refer to a static variable as
LDR r0,[r12,#workspace.screen_mode] rather than
LDR r0,[r12,#12] makes code more readable and easier
to maintain when structure formats are changed.
Compared to the relatively simplicity of ASM, the daunting complexity of ObjAsm discouraged me from learning how to use it. Due to project deadlines I needed to minimise the time spent learning to use a new assembler and concentrate on coding. At the time I did not anticipate needing to use repetitive assembly, though this assumption was later proved wrong.
Taking all these factors into account I eventually decided to use Nick Roberts' ASM, version 4.10. Should it ever become necessary to move the sourcecode to ObjAsm format then this will be considerably easier than if the BASIC assembler had been used, because the ASM source format is broadly similar to ObjAsm and they support many of the same assembler directives.
I used Acorn's ARM Linker version 5.25 to link the
object files generated by ASM. The -AIF
option was used during the development process, to link the
code with a test program and output an Executable AIF30 image. The
-RMF option was used for the final build, to output
the graphics library as a relocatable module.
The two machines used for development were:
| Model name | Acorn Risc PC (c.1994) | Microdigital Mico (c.2000) |
| Processor | 202 Mhz SA-110 rev. K | 56 Mhz ARM7500FE |
| Floating point system | FPEmulator 4.06 (14 Mar 1996) | FPA11 floating point unit |
| Operating system | RISC OS 3.70 (30 Jul 1996) | RISC OS 4.03 (09 Nov 1999) |
| Memory | 20 Mb SIMM + 1 Mb VRAM | 64 Mb EDO RAM |
| Hard disc | 4 Gb | 8.4 Gb |
| Integer benchmark31 | 341,157 Dhrystones/sec | 63,137 Dhrystones/sec |
| FP benchmark | 2,621 kWhetstones/sec | 8,314 kWhetstones/sec |
This pair of machines are actually fairly representative of the RISC OS computers still being used, showing opposite ends of the spectrum. The Mico represents the various third party ARM7500-based machines that have flooded the market since the demise of Acorn Computers Ltd in 1998, whilst the StrongARM Risc PC represents the substantially upgraded Acorn systems still used by computing enthusiasts.
The Risc PC is based around Digital's StrongARM 110 processor, which was first released as an upgrade in 1996.
Because it has a Harvard architecture with separate 16 kb data and instruction caches, code modification is much more expensive than previous ARM processors - cleaning the data cache can take up to half a millisecond (i.e. 100000 processor cycles) and the entire instruction cache must be flushed. [10]
However, it is clocked 5 times faster than any previous ARM, and furthermore many instructions execute in fewer cycles. It implements the ARMv4 instruction set, which includes 64-bit multiply and multiply-accumulate instructions that are unavailable on other RISC OS machines.
No floating point co-processor is available, so floating point instructions must be emulated in software. Given the relative rarity of such instructions, however, this deficiency is more than offset by the high speed of integer arithmetic and general data processing.
Unlike ARM7500-based machines, Risc PCs may include up to 2 Mb of fast dedicated video memory. This plays an important part in the machine's high performance, freeing the main data bus for the use of the processor and other DMA.
To make optimal use of StrongARM, software should avoid using the floating point instruction set if possible, and where appropriate make use of the long multiplication instructions provided. Use of self modifying code is strongly deprecated.
This single chip computer has a rather different architecture from the StrongARM.
An ARM7 core32 is integrated with a video controller, memory/IO controller and FPA11 (floating point unit) on a single chip. Like earlier ARMs, it has a Von Neumann architecture, with a write buffer and 4 kb combined data/instruction cache. Thus there is no penalty for self-modifying code.
For software developers, the significant attributes of this chip are that floating point operations are very fast relative to the FP emulator, yet the main processor clock is relatively slow and is made even slower in high bandwidth screenmodes where up to 50% of data bus bandwidth can be taken by video DMA.
To make optimal use of ARM7500FE machines, software should be designed to run in low bandwidth screen modes and use the floating point co-processor to maximum possible effect (e.g. the FP divide instruction may actually execute faster than an integer divide, since the latter must be implemented as a macro).
The stated disparities in features and architecture between the two target computer systems provide good justification of my design objective that the API of my 3-D graphics library should transparently support different machine-specific implementations.
In the main, the memory management facilities required by my
module were provided through the operating system's
OS_Heap and OS_DynamicArea SWIs.
The static data for each instantiation of the module is held in a small block of relocatable module area of fixed size allocated upon initialisation. This holds state variables such as the current colour, normal vector and matrix mode, and pointers to the matrix stacks and other dynamic buffers.
A separate dynamic area33 holds a heap managed by
OS_Heap, from which blocks for non-static data such as
the render buffer and vertex buffer are allocated. A private
dynamic area is used rather than polluting the RMA because
this allows any substantial amounts of memory used by the
module to be deallocated and returned to the free pool at
termination. If the RMA were used then heap fragmentation
would prevent this.
In order to allow the user to resize the GL module's dynamic
area, a handler for post-grow and pre-shrink events is
installed. This asks OS_Heap to shrink the heap
when the area is reduced (or refuses the movement if this is
impossible), and when the area grows it informs
OS_Heap that the heap may expand.
The GL module only shrinks the heap of its own volition when
rendering of all the buffered graphics is completely by
GL_Finish. By doing this occasionally rather
than whenever a heap block is freed, the performance hit of
constantly expanding and reducing the size of the heap is
avoided, whilst ensuring that excess memory does not linger
in the heap indefinitely.
The vertex buffer extends in 'chunks' which are essentially
separate heap blocks that form a crude forward-linked list.
This linked list structure has been chosen because extending
the vertex buffer contiguously (e.g. using OS_Heap
4) would cause the block to be moved within the heap.
But the vertex records must stay at the same absolute memory
addresses for their entire lifetime, otherwise pointers
within the render buffer would become invalid.
The computational costs of traversing the linked list are
minor. Within the primitive construction routines invoked
upon a call to GL_End, the overhead to check the
vertex buffer read pointer against a chunk limit is just two
instructions per vertex. If the limit is passed then a small
function is invoked to set up the vertex pointer and limit
for the next chunk, or else quit if that was the last chunk
(indicated by link = 0):
|
The render buffer, conversely, is extended contiguously using
OS_Heap 4. In other words it may shift around
within the heap, but it can always be traversed from top to
bottom simply by incrementing a pointer from its current base
address.
Extending a very large buffer in this fashion is not particularly good practice, since it can cause serious heap fragmentation. However, these effects are unlikely to cause real problems on my system given the small number of primitives likely to be stored in the render buffer and the infrequency with which it needs to be extended.
It is important that the render buffer be contiguous in memory, for the implementation of the sort used by painter's algorithm. Theoretically it may be possible to sort data stored in a linked list (sort individual chunks and then merge them?), but I did not investigate any algorithms for doing so. Instead, my sole focus was on finding the fastest sort algorithm possible (see section 7).
In the case of both the render buffer and the vertex buffer, the granularity with which they are extended is deliberately high. The vertex buffer allows room for 64 vertex records per chunk, and the render buffer chunk allows 32 shape records per chunk. Thus, for many simple scenes neither will need to be extended. This is an important factor in performance, since the process of extension is costly and we therefore want to do it as rarely as possible. The speed at which the vertex buffer can be traversed during primitive construction would also be crippled if it were necessary to stop and change to a new VB chunk every few vertices.
I now present a walk through the process of primitive construction, in attempt to explain in detail the operation of the vertex and render buffers.
Imagine that SYS "GL_Begin",5 has been called,
signalling the start of a triangle strip. VB write
pointer is the location where the first triangle strip
vertex will be written, and VB write limit points to
the end of the current VB chunk. The initial values of these
pointers are saved in VB read pointer and VB read
limit, for later use during primitive construction.
There follow six calls to SYS "GL_Vertex" - the
coordinates and colour data of the vertices are unimportant
in the context of this explanation. As each vertex arrives,
it is stored in the vertex buffer at VB write pointer,
which is then incremented for the next vertex.
When VB write pointer meets VB write limit
(after vertex 5), a new VB chunk is allocated and the address
is stored in the link word at VB write limit. When
VB write pointer and VB write limit have been set
up for the new chunk, buffering of vertices continues until
GL_End is called shortly afterwards.
The following diagram shows the state of the vertex and render buffers and their associated pointers as they would appear at this point in time:

The vertex and render buffers and associated pointers as
they appear at the beginning of primitive construction, e.g.
on entry to GL_End
When GL_End is called, the buffered vertices are
read sequentially from VB read pointer. Triangle
primitives are constructed from this stream of vertices and
recorded in the render buffer with pointers back to their
corner vertices.
When VB read pointer reaches VB read limit, it is reset to the base of the second chunk using the link address stored at VB read limit. We detect that we have reached the 'current' (final) vertex buffer chunk, because VB read pointer + VB chunk size = VB write limit. Therefore, VB read limit is set to VB write pointer rather than the end of the chunk.
Construction of triangle primitives continues using vertex 6 from the second VB chunk, until VB read pointer reaches VB read limit for the second time. We detect that we have reached the end of the stored vertices rather than the end of the current block, because VB read limit = VB write pointer.
The following diagram shows the state of the vertex and render buffers and their associated pointers as they would appear at this point in time34:

The same imaginary scenario as it would appear at the
close of primitive construction, e.g. on exit from
GL_End
The painter's algorithm requires surfaces to be sorted by depth prior to rasterisation, so that surfaces can be painted to the screen in decreasing depth order.
A test program showing the sorting of many graphics primitives by depth
Because of the serious impact that an inefficient sort (such as bubble sort) would have on the system's performance, I did some research on the relative performance and suitability of different sorting algorithms, I found that two sorting algorithms most often recommended for depth sorting were 'heap sort' and 'quick sort'.
According to Todd Sundsted [23] "The most efficient, general
purpose sort is one based on C.A.R. Hoare's quicksort
algorithm." Robert Ohannessian disagrees, favouring heap sort
over quick sort: "The Quick Sort, however, is less than
optimal as we shall see... Unlike Quick Sort, [heap sort's]
worst case is ![]() , making it very, very
useful." [22]
, making it very, very
useful." [22]
"Quicksort is one of the fastest and simplest sorting algorithms. It works recursively by a divide-and-conquer strategy."[24] One of the values in the array is chosen as the 'pivot' - all values less than the pivot are moved to its left, and all values greater than it to its right. The algorithm is then applied recursively to the left and right halves of the array, yielding smaller and smaller subsets until the whole array is sorted.
Quick sort's best case time complexity is ![]() , obtained when each partitioning produces two parts of
equal length. In the worst case scenario (where the
partitioning is maximally unbalanced) the complexity is
, obtained when each partitioning produces two parts of
equal length. In the worst case scenario (where the
partitioning is maximally unbalanced) the complexity is ![]() - as bad as bubble sort.
- as bad as bubble sort.
Heap sort is based upon a left-complete binary tree, where each node has a value greater than that of its children. When this is true, the tree is a 'heap', and the process of making sure that each parent node is greater than its children is called 'heapification'. This structure can be organised in memory as a conventional array by laying the tree out flat, row by row. Once the array contents have been 'heapified', the root node (guaranteed to be the largest value) is removed to a section of the array that is designated 'sorted'. The remainder of the array is then 'reheapified' so that the the new root node is now the second largest value... this cycle of removal of the root node and reheapification of the remainder is repeated until all the values are sorted.
Given that timing analysis shows quick sort's best case to be only as good as heap sort's worst case, when I wrote an optimised implementation of heap sort I fully expected it to outperform the non-optimised quick sort that I had compiled with minimal attention from some example C sourcecode.
I was therefore rather surprised to find that quite the reverse was true, as shown by the following timings on data sets of different sizes. The test data was an array of 32-bit integers generated randomly for each comparative test run. The same test data was sorted by each algorithm to ensure a fair comparison35, and a subset of the sorted set was output to show that the two algorithms were producing consistent results.
| Number of elements | Quick sort | Heap sort |
|---|---|---|
| 1,000 | 0.01s | 0.01s |
| 100,000 | 1.49s | 2.91s |
| 1,000,000 | 27·86s | 37·80s |
| 2,000,000 | 70·76s | 72·93s |
| 3,000,000 | 149·44s | 122·76s |
As can be seen from these timings (each averaged over several runs), the heap sort did not even begin to outperform the quick sort until there were more than 2 million elements in the array.
I did eventually find another voice to give credence to my
findings - "There are sorting algorithms with a time
complexity of ![]() even in the worst case, e.g.
Heapsort and Mergesort. But on the average, these
algorithms are by a constant factor slower than
Quicksort." [24] The explanation appears to be that
although heap sort is theoretically less complex than quick
sort, it is unstable. In other words, it causes more
data swaps when re-ordering the array. It can be imagined
that this would cause a major impact on performance,
particularly since the test system was a 200 Mhz processor
coping with a 16 Mhz memory bottleneck.
even in the worst case, e.g.
Heapsort and Mergesort. But on the average, these
algorithms are by a constant factor slower than
Quicksort." [24] The explanation appears to be that
although heap sort is theoretically less complex than quick
sort, it is unstable. In other words, it causes more
data swaps when re-ordering the array. It can be imagined
that this would cause a major impact on performance,
particularly since the test system was a 200 Mhz processor
coping with a 16 Mhz memory bottleneck.
I felt that this deficiency in the heap sort algorithm would be compounded when swapping real data (i.e. render buffer records, at 32 bytes each) rather than plain integer values. Also, the likelihood of the render buffer ever containing 2 million primitives is virtually nil. Everything pointed to quicksort as the better choice.
The first thing to happen is that various information about
the current screen mode and VDU drivers state is read, by
calling OS_ReadVduVariables with a pointer to a
list of variable numbers. This tells us the configuration of
the frame buffer, its address in memory, the screen
resolution, the size in bytes of the whole screen and that of
an individual screen line. The bounding coordinates of the
graphics window and the position of the graphics origin are
also obtained.
If the current screen mode is inappropriate for rendering, e.g. it is a teletext or other non graphics mode, or a graphics mode with less than 8 bits per pixel, then the module returns a polite error message "Cannot plot in this screen mode". The flashing text cursor is removed from the screen for the duration of the rendering process, since this might interfere with graphics plotting.
The obvious way to draw lines is to calculate the line's gradient (requiring a division) and use fractional x/y increments. However, for long line segments accumulated rounding errors "can cause the calculated pixel positions to drift away from the true line path", and furthermore the necessary gradient division and floating-point arithmetic are costly. [2]
Instead, the GL module plots lines using an accurate and
efficient algorithm developed by Bresenham, that uses only
integer calculations. Sampling a line at unit ![]() intervals, an integer 'decision parameter'
intervals, an integer 'decision parameter' ![]() determines for a given pixel
determines for a given pixel ![]() whether the next pixel to plot should be
whether the next pixel to plot should be ![]() or
or ![]() .
.
Successive values of ![]() are obtained
recursively using incremental integer calculations. The
algorithm for lines with a positive gradient < 1 may be
summarised as follows, where
are obtained
recursively using incremental integer calculations. The
algorithm for lines with a positive gradient < 1 may be
summarised as follows, where ![]() and
and ![]() are the horizontal and vertical
distances between the line's endpoints (from Hearn and
Baker):
are the horizontal and vertical
distances between the line's endpoints (from Hearn and
Baker):
![]()
For each ![]() along the line, starting at
along the line, starting at ![]() :
:
If ![]() , next point to plot is
, next point to plot is ![]() , and
, and
![]()
Otherwise, next point to plot is ![]() , and
, and
![]()
This algorithm is generalised to lines with arbitrary slope by selecting one of four plotting routines, depending on the relative positions of the line endpoints A and B:
line_pos_steep plots a line with positive
gradient greater than 1, by scanning up the screen line by
line and calculating successive x positions (y-major).
line_pos_shallow plots a line with positive
gradient less than or equal to 1, by advancing across the
screen pixel by pixel and calculating successive y
positions (x-major).
line_neg_steep plots a line with negative
gradient less than -1, by scanning down the screen line by
line and calculating successive x positions (y-major).
line_neg_shallow plots a line with negative
gradient greater than or equal to -1, by advancing across
the screen pixel by pixel and calculating successive y
positions (x-major).
Two signed differences ![]()
![]() are calculated, in order to
determine the direction of the line.
are calculated, in order to
determine the direction of the line.
Firstly, if B is left of A (i.e. ![]() ) then the two endpoints are reversed. This immediately
eliminates one half of the eight possible octants in which a
line can lie (the shaded area on the diagram below), by
guaranteeing that all lines are drawn from left to right (A
to B).
) then the two endpoints are reversed. This immediately
eliminates one half of the eight possible octants in which a
line can lie (the shaded area on the diagram below), by
guaranteeing that all lines are drawn from left to right (A
to B).
If B is higher or same as A (i.e. ![]() ) then the line is identified as having a positive
slope:
) then the line is identified as having a positive
slope: line_pos_shallow is called if the
gradient is 1 or less (i.e. ![]() ), otherwise
), otherwise line_pos_steep is called.
If B is lower than A (i.e. dy<0) then the
line is identified as having a negative slope:
line_neg_shallow is called if the gradient is -1 or
greater (i.e. ![]() ), otherwise
), otherwise
line_neg_steep is called.
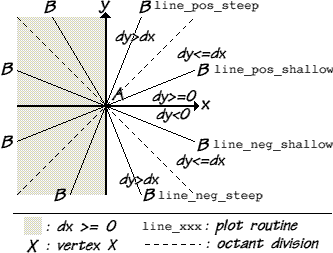
Selection of Bresenham plotting code, depending on line slope
There is a reason that I implemented four separate plotting routines rather than a single routine for x-major lines and one for y-major lines, both generalised to accept signed increments:
The procedure for clipping lines to the graphics window is different, depending on whether the line is being drawn upwards or downwards. For negative slope lines (those in the bottom right quadrant of the diagram) plotting terminates when the line passes the bottom or righthand side of the clipping window, whereas for upward facing lines (in the top right quadrant) line plotting terminates when the line passes the top or righthand side of the clipping window.

Output from a test program that allows the vertices of a 3-segment line loop construct to be moved about the screen. The lines have been clipped to the current graphics window.
The first step in triangle rasterisation is to find which of the corner vertices A, B and C has the lowest y coordinate. The vertices are rearranged if necessary to ensure that vertex A is lowest (as with lines, this allows greater use of generic code). Vertex A will be the starting point for plotting the triangle.
Next, plane equations are used to determine which of the two higher vertices B and C is 'left' and which is 'right', relative to each other:
![]()
If the above expression evaluates as false, then vertex B is not leftmost and it is swapped with vertex C. We now know the endpoints of the initial lefthand (A to B) and initial righthand (A to C) edges of the triangle, which allows us to calculate the left and right gradients (as fractional x increments per scanline).
The final step before we can draw the triangle is to find which of vertices B and C is the 'middle' vertex and which is the 'top' vertex. This is established by a simple comparison of y coordinates.

Scan conversion of the lower half of a triangle, by
flat_tri_segment
The bottom and top halves of the triangle are drawn
separately by calling a generalised routine
flat_tri_segment, which plots successive pixel spans
of a polygon between any two y-major edges. The necessary
parameters are a colour, upper & lower y bounds
and the origin and gradient of the segment edges. The edges
are specified as initial left x and right x
coordinates and a fractional increment to be applied to each
side per unit y. For fractional accuracy, all x
coordinate calculations use fixed-point q=12 form (accurate
to ![]() ).
).
The bottom half is plotted from ![]() to
to ![]() if B is the 'middle' vertex,
otherwise from
if B is the 'middle' vertex,
otherwise from ![]() to
to ![]() . Upon reaching a height parallel to the 'middle' vertex
a new gradient is calculated for whichever edge, left or
right, spans from the 'middle' vertex to the 'top' vertex.
(The righthand edge C to B in the
example above.) Finally,
. Upon reaching a height parallel to the 'middle' vertex
a new gradient is calculated for whichever edge, left or
right, spans from the 'middle' vertex to the 'top' vertex.
(The righthand edge C to B in the
example above.) Finally, flat_tri_segment is
called again to plot the top half of the triangle.
Hearn and Baker: "This intensity-interpolation scheme, developed by Gouraud and generally referred to as Gouraud shading, renders a polygon surface by linearly interpolating intensity values across the surface." [2]
If perspective-correct shading is not required then colours may be calculated iteratively using a fixed increment for red, green and blue colour components. Perspective-correct interpolation of either colours or texture coordinates across a polygon surface is very much more costly36, so it is fortunate that linear approximation is generally adequate where individual surfaces do not span large z distances.
My Gouraud triangle renderer was implemented by extending the basic mono-colour triangle-plotting routine I had implemented before, with a lot of extra code to calculate fractional increments for colour components across each pixel span, and along each outside edge between vertex colours.
I managed to cut down on the number of individual divisions
necessary, by using the technique described by ARM Ltd for
instead multiplying by the reciprocal of the divisor [8]:
Having calculated ![]() in fixed point q=16 form, I
can multiply by the red difference
in fixed point q=16 form, I
can multiply by the red difference ![]() to get the red increment per line, multiply by the
x difference
to get the red increment per line, multiply by the
x difference ![]() to get the x
increment per line... and similarly for the green and blue
components.
to get the x
increment per line... and similarly for the green and blue
components.
Another clever trick used is that of packing the intensity value and increment-per-line for a colour component into a single register. Each part is stored in fixed point q=8 form, with the increment occupying the top 16 bits of the intensity value. This massively reduces the frequency of variable spillage to memory, and hence the complexity of the whole routine. Updating the edge colour components upon moving up a scanline is reduced to:
|
Because pixel colours vary across the triangle, it is no
longer possible to call ColourTrans just once before
plotting, to obtain a single colour number for an 8bpp screen
mode. Fortunately a scheme has been implemented to avoid the
alternative of calling
ColourTrans_ReturnColourNumber for every pixel
plotted.
The 24bpp palette entry and corresponding colour number are retained from the previous pixel plotted. If the new palette entry calculated from the colour components and increments matches the previous colour, then the old colour number is used again. Thus when plotting a shaded span of pixels ColourTrans is only called once per change of colour:
|
(A far preferable solution would be to have an internal colour lookup table that could be consulted as frequently as necessary, at much less than the cost of a SWI call. This has not yet been implemented, however.)
Gouraud shading is inevitably slower than flat shading, because of the extra division required to determine colour gradients across pixel spans, and also because holding colour components and their increments in addition to all the other working data inevitably puts a severe strain on register allocation.

Output from a test program that allows the vertices of a gouraud-shaded triangle to be moved about the screen, and the R,G,B colours at each vertex to be updated. The triangle has been clipped to the current graphics window.
After all the primitives in the render buffer have been rasterised, both the render buffer and the vertex buffer are deallocated. In the case of the render buffer this is simple matter of freeing the block. In the case of the vertex buffer, the linked list of VB chunks must be traversed from the bottom upwards, freeing each block in turn.
The most general form of optimisation performed was careful allocation of register usage, so that variables are not spilled to memory if at all possible. If variables must be spilled to memory then preferably they should be the values that are accessed relatively infrequently.
A C compiler allocates a fixed amount of stack space for
local non-register variables on function entry. These
non-register variables are then loaded and stored as needed,
using individual LDR/STR
instructions.
When hand-coding assembly language you tend use the stack in
a more conventional FIFO37 fashion. A common action is to push
whole groups of variables onto the stack in a single motion,
for the duration of some subtask. This can be done relatively
cheaply using a single STM instruction, giving
the following benefits over a sequence of individual
STR instructions: "The code is smaller (and thus will
cache better...", and "...an instruction fetch cycle and a
register copy back cycle is saved for each LDR
or STR eliminated." [9]
Because the ARM processor has no divide instruction, a division routine is a common feature of most RISC OS programs of any complexity. Essentially they come in two varieties - rolled and unrolled. In unrolled implementations the inner loop is implemented at assembly-time rather than in the output code. Replication of the body of the loop results in very much larger output, but the branch back to the beginning is eliminated.
I decided against using an unrolled division loop for two reasons - firstly I was mindful of the warning in the ARM cookbook that "it doesn't always gain anything, and in some situations can reduce performance" [9], and also because an unrolled loop would make the code too bulky for inclusion in a macro38.
I wanted to use a division macro rather than a real subroutine not so much because of the cost of the call (a branch is relatively cheap on ARM), but because of the indirect cost of martialling arguments in specific registers (which may be being used for other purposes) and of the subroutine saving any registers that it corrupts, ignorant of whether or not this is actually necessary.
Use of a macro allowed me more control over which registers were the divisor and dividend, which was the destination register for the quotient, and which registers could safely be corrupted by the operation. Given the choice, I found that I could invariably manage to find a couple of scratch registers without resorting to using the stack as a subroutine would do.
|
Since there is no point re-inventing the wheel, my division macro is based upon the divide-and-remainder code given in the Acorn Assembler manual [4]. At only fifteen instructions (for unsigned division), it is not too onerous for the code to be included every time it is used.
It is actually quite difficult to print out debugging and
trace information from an assembly language program compared
to, say, calling printf() from a C program. The
operating system provides a number of SWIs that aid assembly
language programmers in this task, chiefly
OS_Write0 (write text string pointed to by R0),
OS_WriteS (write embedded text string) and
OS_NewLine (write line feed/carriage return).
The OS_ConvertHex8 and
OS_ConvertInteger4 SWIs are also invaluable for
converting integer values into strings for output to the
screen, but there is unfortunately no equivalent call that
will output values with a fractional component. This proved
to be a major stumbling block, since fixed-point fractional
values are predominant in my GL module.
The solution eventually adopted is quite grotesque: The
fixed-point value to be output is first transferred to a
floating-point register and divided by 2exponent,
then stored to memory in packed decimal format
(STFP). A complex subroutine is invoked to
laboriously print the fractional value in standard form,
character by character:
|
Obviously, frequently typing out complex debugging code such
as that shown above would have been a complete nightmare,
almost certainly introducing more bugs than it would have
enabled me to find. Therefore, all the common debugging/trace
operations are encapsulated in helpfully named macros such as
tracelabel, printdec,
printhex and printfxp.
The use of macros allowed me to output large amounts of
verbose debugging and trace information, whilst maintaining
relatively clean-looking and readable code. By bracketing
each macro definition by IFDEF trace... ENDIF
assembler directives, all that is required to produce a clean
version of the module is to undefine a single symbol.
The only real blot on this picture is that ASM does
not appear to accept text strings as macro parameters.
Fortunately, OS_WriteS allows plain text strings
to be output without too much pain, mainly due to the fact
that invocation requires no registers (the string to print is
embedded in the program code right after the SWI
instruction).
27 Acorn's Desktop Debugging Tool.
28 ARM Object Format, the standard intermediate format for code output by language processors.
29 Whilst Nemo (comp.sys.acorn.programmer) gives a method of creating ObjAsm constructions similar to the structures explicitly supported by ASM, the equivalent ObjAsm syntax appears more complicated.
30 ARM Image Format, the usual format for executable program code under RISC OS.
31 These benchmarks were measured using SICK v0.94, a reputable system analyser and speed indexer.
32 Note that this is distinct from the ARM7M, which first introduced the long multiply instructions supported by the StrongARM.
33 Dynamic areas are large areas of memory such as the free pool, the module area and the screen memory, for which the mapping of logical to physical addresses is managed by hardware. Thus, their size can be changed transparently without the base address appearing to change.
34 For the sake of clarity, I have drawn the link between primitives and vertices using arrowed lines going from vertex buffer to render buffer. Whilst this may be thought of as the direction of data flow, the actual pointer reference goes the other direction.
35 The speed of sorting can vary considerably depending on the distribution of test values in a particular data set, and how unsorted the set is. This is especially true for quicksort, where choosing the wrong pivot will cause all the data to be moved.
36 Especially given the ARM's lack of a divide instruction - the architecture was designed for normal programs where divisions are rarely necessary, not for rendering perspective-correct polygons at one division-per-pixel!
37 First-In-First-Out. The conventional stack model where items only enter and leave at the head of the stack, by 'push' and 'pull' operations. Items further down the stack are temporarily inaccessible until any items pushed on after them have been pulled off.
38 There was also the 'minor consideration' that ASM doesn't actually support repetitive assembly(!) This is probably symptomatic of the fact that unrolling loops has gone out of fashion.